2×n 크기의 직사각형을 1×2, 2×1 타일로 채우는 방법의 수를 구하는 프로그램을 작성하시오.
아래 그림은 2×5 크기의 직사각형을 채운 한 가지 방법의 예이다.

입력 : 첫째 줄에 n이 주어진다. (1 ≤ n ≤ 1,000)
출력 : 첫째 줄에 2×n 크기의 직사각형을 채우는 방법의 수를 10,007로 나눈 나머지를 출력한다.
<풀이>
타일을 채워나갈 수 있는 방법은 두 가지가 있다.
1. 세로로 길게 채우는 방법
2. 가로로 눕혀서 두 개를 채우는 방법
세로 길이는 항상 2 크기를 지니고 있기 때문에 가로의 경우만 보겠다.
먼저 첫 번째 방법 처럼 세로로 길게 채우는 방법을 보면,
세로로 길게 세워서 채우는 경우에는 2x1 크기로 가로의 길이가 1만큼만 늘어난다.
반면 두 번째 방법의 경우에는, 가로로 두 개의 타일을 채우면 2x2 크기로 가로의 길이가 2만큼 늘어나게 된다.
예를 들어, 2x4 크기의 직사각형을 채운다고 가정을 해보겠다. 아까 타일을 채워나갈 수 있는 방법 두 가지를 이용해 보자면,
1번 방법 이용 : 2x3 타일에 1개를 덧 붙인다.
2번 방법 이용 : 2x2 타일에 2개를 덧 붙인다.
즉, 2x4 크기의 타일을 채우는 방법은 2x3과 2x2 크기의 타일을 채운 방법의 수를 더한 값이 된다.
(왜냐하면, 타일을 채우는 방법은 세로로 1개를 붙이는 방법과 2개를 가로로 눕혀서 채우는 방법 뿐이기 때문)
이 것을 점화식으로 세운다면,

이 것을 활용하여 코드를 짠다면 이런 식으로 짤 수 있다.
import java.util.*;
public class dp_2n {
static public void main(String args[]){
Scanner s = new Scanner(System.in);
int n = s.nextInt();
int[] dp = new int[n+1];
dp[0] = 1;
dp[1] = 1;
if(n>=2){
for(int i = 2; i <= n; i++){
dp[i] = (dp[i-1] + dp[i-2]);
dp[i] %= 10007;
}
}
System.out.println(dp[n]);
}
}여기서 dp[i] %=10007;을 for문 안에 넣은 이유는 오버 플로우가 발생할 수도 있기 때문에, for문 안에 넣은 것이다.
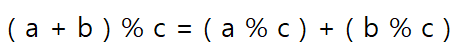
위의 식을 보면 a와 b의 합을 c로 나눈 나머지 값이나 a, b를 따로 나눈 나머지 값이나 동일하다. 그렇기 때문에 오버플로우를 방지하고자 for문 안에 % 식을 넣었다.
'Study > Algorithm' 카테고리의 다른 글
| [1932] 정수 삼각형 (0) | 2020.05.13 |
|---|---|
| [14501] 퇴사 (0) | 2020.05.12 |
| [2225] 합분해 (0) | 2020.05.08 |
| [2293] 동전1 (0) | 2020.05.07 |
| [9461] 파도반 수열 (0) | 2020.05.07 |




댓글